Unsere Webseite verwendet nur Cookies, die technisch notwendig sind und keine Informationen an Dritte weitergeben. Für diese Cookies ist keine Einwilligung erforderlich.
Weitere Informationen erhalten Sie in unserer Datenschutzerklärung.
Einführung in die Quantenphysik (Dr. Ulrich Noll)
Die Muttersprache lernt man, indem man sie verwendet. Die Bedeutung der Sprachinhalte werden einem beim Sprechen nach und nach bewußt.
Physik kann man wie eine Muttersprache lernen, lassen Sie sich darauf ein!
Erforderliche Vorkenntnisse:
Vektoraddition nach der Parallelogramm-Regel, auch in der Kurzfassung (Dreiecksregel).
Das 5-Regeln-Rezept zur richtigen Vorhersage
"aller" quantenmechanischer Experimente
Ein anschauliches Modell für eine nicht anschauliche Wirklichkeit
1. Stellen Sie eine Quelle Q auf, die Quantenobjekte abgibt, oder finden Sie den Ort der Quelle Q, mit der das Experiment geplant ist!
2. Entscheiden Sie sich für einen Zielpunkt Z, in dem Sie das Experiment auswerten. DerVersuchsaufbau besteht in der Regel aus "Hindernissen" (Schlitz = Einfachspalt, Doppelspalt, Spiegel, Linsen, Glasscheiben = planparallele Platten, Prismen, Salzkristall bei Röntgenstrahlen ...)
3. Finden Sie alle möglichen (nicht unterscheidbaren) "Zeigerlinien" = Pfade zwischen der Quelle Q und dem Ziel Z für das vorgegebene Experiment. Das sind zunächst1 die relativ kürzesten Verbindungen, die der Versuchsaufbau (das Hindernis) zulässt. (Vgl. Abb. 1, 2)
1Dieses "zunächst" verstehen Sie, sobald die geradlinige Ausbreitung des Lichts besprochen ist.
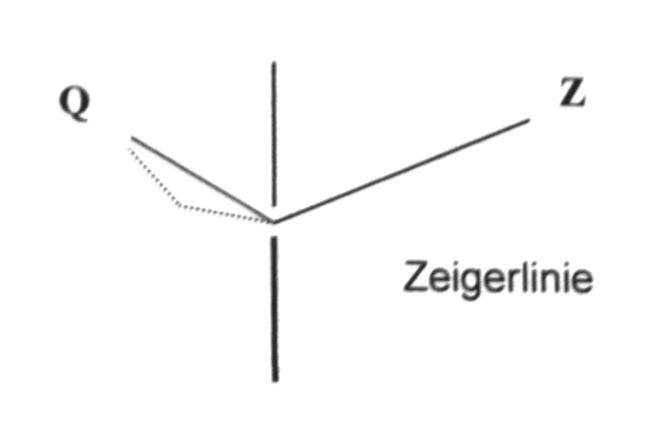 |
Abb. 1: Einzelspalt |
 |
Abb. 2: Spiegel Zeigerlinien zwischen Quelle S und Ziel P für einen ebenen Spiegel aus den Elementen |
4. Alle Zeigerlinien mit dem Steckenrad abfahren, und die Zeigerendstellung ermitteln:
Die Quelle sendet Felder oder Objekte mit einer charakteristischen Wellenlänge lambda aus.
Eine Lichtquelle sendet Licht = Lichtquanten = Photonen = kleinste Lichtportionen aus. Jedem Quantenobjekt, auch dem Elektron aus einem glühenden Draht, kann man eine Wellenlänge zuordnen, wenn man dessen Impuls p = m × v kennt: lambda = h/p = h/mv; h= Planck'sches Wirkungsquant.
Für jedes zu beschreibende Quantenobjekt ist ein Rad (an einem Haltestiel) zu besorgen, bei dem der Radumfang genau lambda ist. Auf dem Rad wird ein Zeiger mit der Länge 1 (eins) angebracht (vgl. Abb. 3) Wir nennen dieses Rad wegen des Haltestiels Steckenrad.
Jede Zeigerlinie wird mit dieses Steckenrad abgefahren (vgl. Abb. 3). An der Quelle zeigt der Zeiger nach oben, dann dreht er sich mit dem Rad, bis er am Zielpunkt Z stehenbleibt.
Die Zeigerendstellung legt einen Winkel phi fest, den wir Phase nennen.
Unser Steckenrad ist ein Wellenlängenzähler (lambda -Zähler) und zugleich ein Phasenanzeiger: Der Zeiger des Steckenrads soll sich ja jeweils einmal drehen, wenn das Quantenobjekt auf dem betreffenden Pfad (der Zeigerlinie) die Strecke lambda zurücklegt bzw. zurücklegen würde.
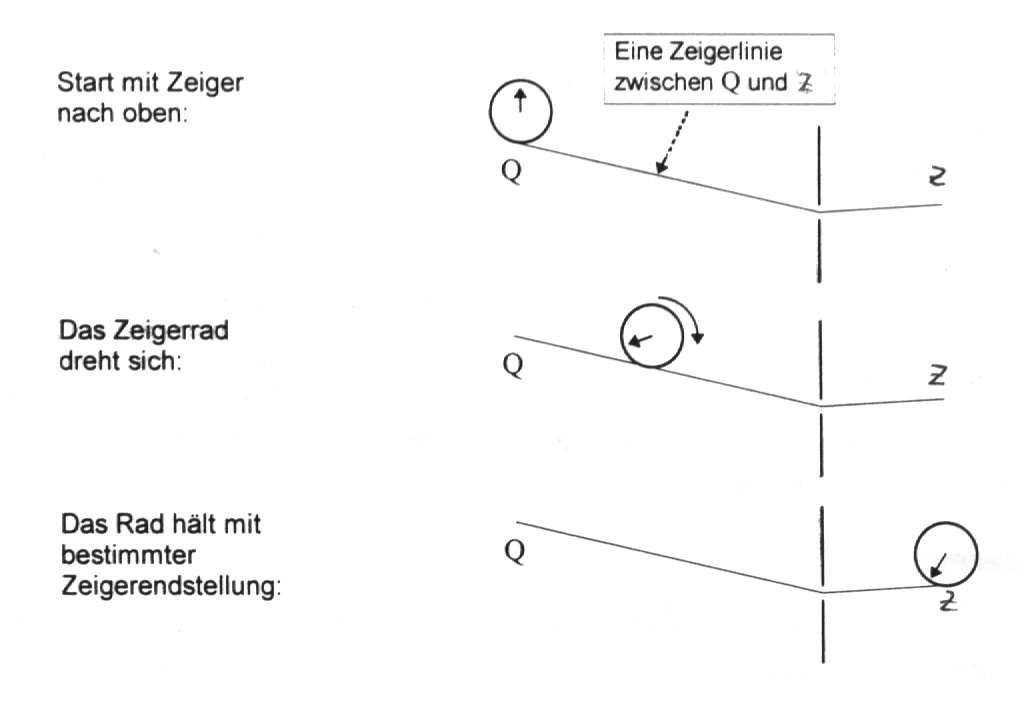 |
Abb. 3: Für jede Zeigerlinie wird die Zeigerendstellung gewonnen. |
5. Zeiger im Ziel nach der Parallelogrammregel addieren
und den resultierenden Zeiger quadrieren!
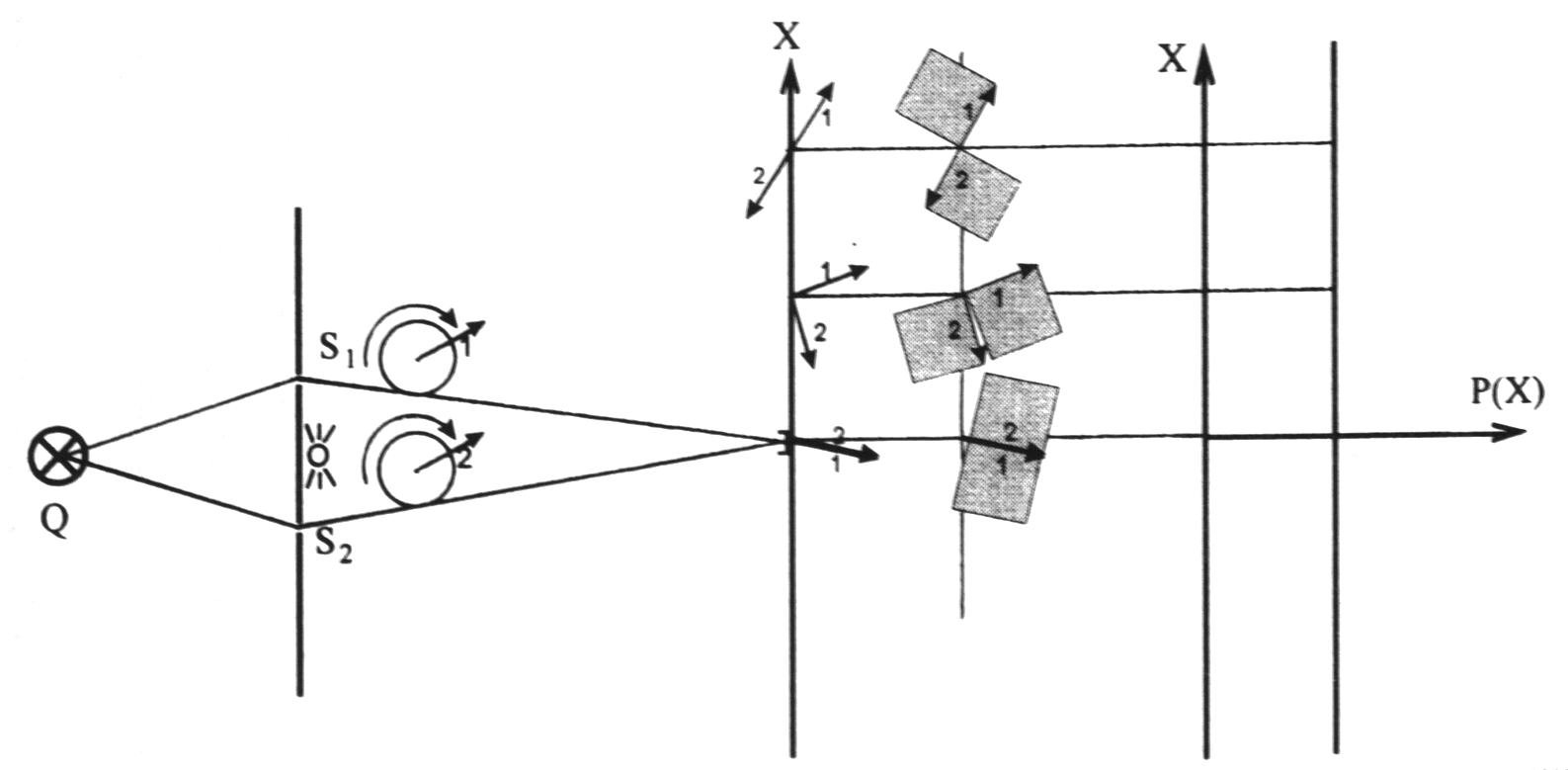
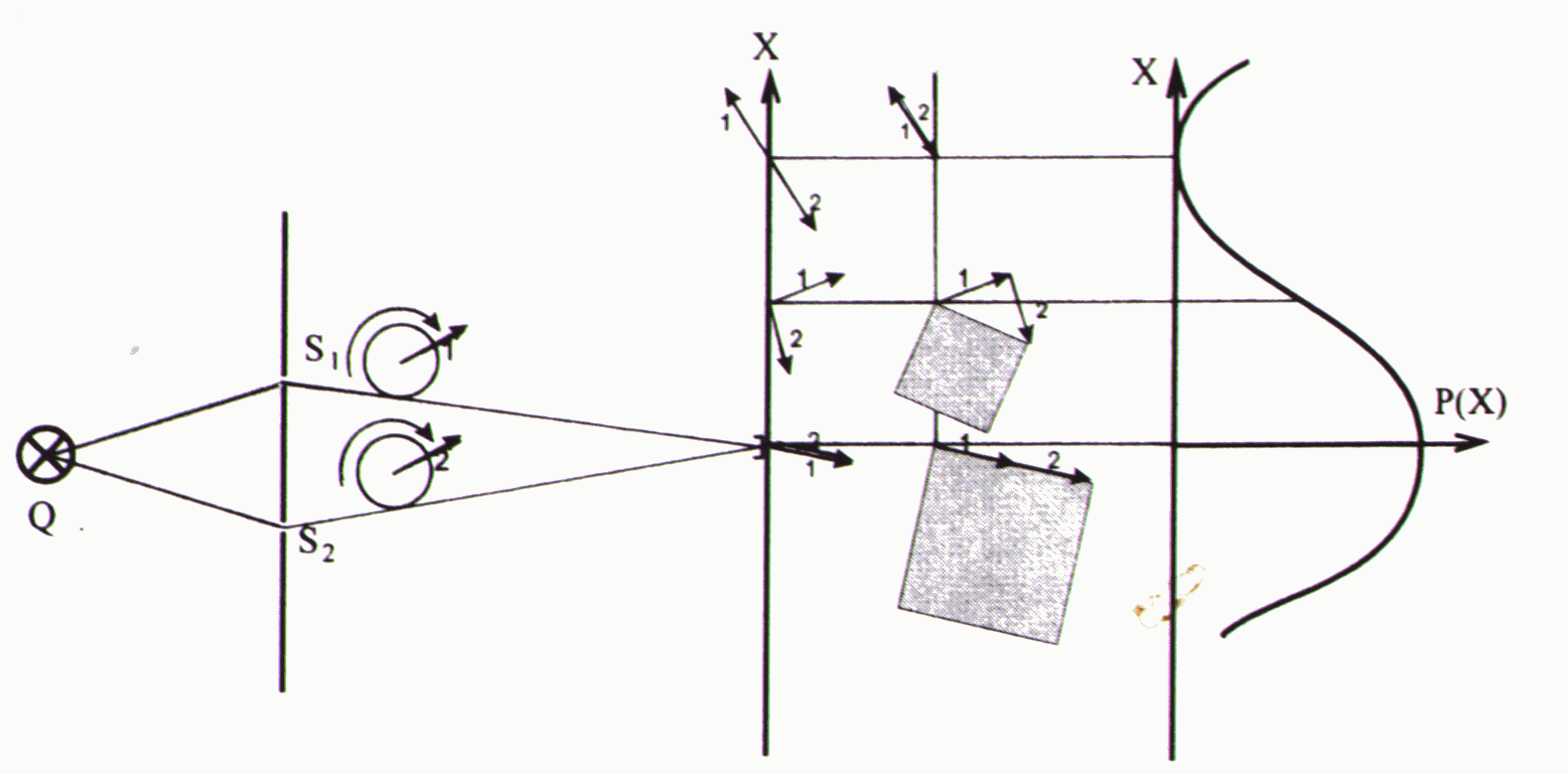
Betrachten Sie nachfolgendes Beispiel: Doppelspalt-Experiment mit geeignetem (kohärentem) Licht
Das Beispiel ist vergleichbar mit der Überlagerung von Schallwellen aus zwei gleichartig gespeisten Lautsprechern oder Wellenbildern von zwei Steinen, die gleichzeitig nebeneinander ins Wasser geworfen werden.
Für alle Zeigerlinien (hier sind es nur zwei) werden die Pfeile im Zielpunkt nach der Parallelogrammregel addiert. Der sich ergebende Summenzeiger (resultierende Zeiger) wird quadriert und stellt die (unnormierte) Nachweiswahrscheinlichkeit für das betrachtete Quantenobjekt dar.
 |
|
Abb. 4: Doppelspalt Erarbeitung der Zeiger-Regeln: Mehrere Zielpunkte werden nacheinander betrachtet. Sie sind hier nicht mit Z sondern X bezeichnet.S1S2 stellt den Doppelspalt dar. |
Wiederholung - Gebrauchsanleitung für das Steckenrad: "Zeigerformalismus":Man beachte, dass bei allen Phänomenen der Quantenphysik Quellpunkt Q und Zielpunkt Z stets vorgegeben sein müssen. Da man prinzipiell nicht vorhersagen kann, auf welcher Bahn das nächste Quantenobjekt zum Ziel Z gelangt, ordnet man jeder möglichen Bahn, die das unteilbare Quantenobjekt von Q nach Z durchlaufen könnte, eine Zeigerlinie und somit einen rotierenden Zeiger als lambda -Zähler zu und addiert alle so ermittelten Zeiger im Zielpunkt Z. Das Quadrat des resultierenden Zeigers im Zielpunkt ist ein Maß für die Energieeinstrahlungsintensität in der Wellenoptik; in der Quantenphysik gibt dieses Quadrat die Nachweiswahrscheinlichkeit für das Quantenobjekt im Zielpunkt an.
Vertiefung: Zusatzregel für Neugierige
Wird beim Doppelspaltexperiment kontrolliert, durch welchen Spalt (1 oder 2) ein Quantenobjekt gekommen ist, muss die Auswertregel 5 geändert werden:
6. Bei Kontrolle des Quantenobjekts (bei unterscheidbaren Zeigerlinien): Pfeile im Ziel erst quadrieren dann addieren (nachfolgende Abbildung 5 verdeutlicht die Vorgehensweise)
Solange beim Doppelspaltexperiment nicht sicher ist, durch welchen Spalt das Quantenobjekt ging, nennen wir die Zeigerlinien ununterscheidbar. Regel 5 ist anzuwenden! Werden durch einen experimentellen Eingriff die Zeigerlinien unterscheinbar, muss nach Regel 6 vorgegangen werden.
|
|
|
Abb. 5: Kontrollierter Doppelspalt Zeigerregel für experimentell unterscheidbare Zeigerlinien |
Vom Rezept zur Ausdeutung!
Es gilt heute in der Quantenphysik, die aus der klassischen Physik stammenden ungeeigneten, "falschen" (auf Widersprüche führenden) Vorstellungen von Anfang an zu vermeiden. Der Dualismus Welle-Teilchen kann widerspruchsfrei vermieden oder "aufgelöst" werden.
Franz Bader: Physiker nehmen anschauliche Widersprüche leicht hin, da sie mit dem mathematischen Formalismus widerspruchsfrei umgehen.
Albert Einstein: Bei meiner Art zu denken spielen Worte keine Rolle; es ist eher ein assoziatives Spiel mit mehr oder weniger klaren Bildern.
Was bedeutet der Zeigerformalismus? Wozu dieses 5-Regeln-Steckenrad-Rezept?
Bei neuen Wörtern oder gar einer Sprache, die man gelernt hat, will man wissen, was die Ausdrücke im Einzelnen bedeuten. Mit dem Zeigerformalismus kann man Experimente richtig voraussagen, Inhalte und Phänomene erschließen (siehe Quantenhänomene). Dies erfolgt im Tun genau so wie man es von der Muttersprache her kennen!
Alltägliches : Wasserwellen - Gebogene Sonnenstrahlen - Spiegel - Linsen
Mit vier Aufgaben soll der sich selbst erschließende Erkenntnisweg verdeutlicht werden.
1. Werfen Sie die beiden (wellenliefernden) Steine aus dem Eingangsexperiment nicht gleichzeitig ins Wasser, sondern so, dass der zweite Stein gerade ein Wellental hervorbringt, solange der erste einen Wellenberg auslöst.
Wie ist dieser Versuchsansatz in die Modell-Sprache (Zeigerformalismus) zu übersetzen? Antworten Sie auch, wenn Sie vielleicht zunächst noch glauben, nicht zu wissen, was die Elemente/Worte bedeuteten.
Das zweite Steckenrad startet nicht mit dem Zeiger nach oben, sondern mit dem Zeiger nach unten.Wieder wird in Zielpunkten Auslöschung und Verstärkung auftreten, nur eben an anderen Stellen.
2. Betrachten Sie das vertraute Phänomen "Licht breitet sich geradlinig aus" in ihrer neuen Modell-Sprache. (Feynman S. 67 Abb. 32, Bader-Programm
Die Wahrscheinlichkeit eines Ereignisses errechnet sich, indem man die Pfeile für sämtliche Wege addiert, auf denen das Ereignis eintreten kann (so gewunden diese auch sein mögen).
Es ist festzuhalten, dass der den geradlinigen Weg über D darstellende Pfeil (Feynman Abb. 32) allein nicht genügt, um die Intensität im Ziel zu begründen. Offensichtlich leisten die benachbarten, nahezu geradlinigen Wege – zum Beispiel über C und E – ebenfalls einen wichtigen Beitrag. Das bedeutet, dass sich das Licht in Wirklichkeit nicht nur geradlinig ausbreitet; es "schmeckt" in die Nachbarpfade ringsherum "hinein".
3. Lernen Sie das Reflexionsgesetz des Spiegels "Einfallswinkel gleich Ausfallswinkel" in der neuen Sprache kennen. (Feynman S. 55 Abb. 24, Bader-Programm
Den größten Betrag zur Länge der Resultierenden leisten eindeutig die Pfeile E bis I (Feynman Abb. 24) , die allesamt fast in die gleiche Richtung weisen. Das Photon tastet sich aber auch hier in alle Nachbarpfade. Auf der Ihnen bekannten Strecke "Einfallswinkel gleich Ausfallswinkel" fällt im Wesentlichen die Entscheidung, ob ein Photon vom Spiegel zurückgeworfen wird oder nicht.
Es soll belegt werden, dass auch die Ränder des Spiegels A-B-C, K-L-M reflektieren – diese Reflexionen nur nicht in Erscheinung treten, weil die Einzelpfeile sich hier schließen und nichts zur Gesamtintensität beitragen.
Nehmen wir an, wir würden den Spiegel überall dort auskratzen, wo die Pfeile in Richtung "Uhrzeigersinn" tendieren, so dass einzig die Bereiche übrig bleiben, deren Pfeile in die andere Richtung "Gegenzeigersinn" weisen. Unserer Theorie zur Folge müssten wir jetzt eine starke Reflexion beobachten können! In der Tat können wir das – die Theorie ist richtig! Ein solcher Spiegel wird als Reflexionsgitter bezeichnet und wirkt wahre Wunder. Oder ist es nicht verwunderlich, dass ein Spiegelstück, von dem man sich keine Reflexion erwartet, mit einemmal Licht reflektiert, nur weil man einen Teil des Spiegels ausgekratzt hat?
(Realexperiment mit cm-Wellen: Vorschlag von Bader-Programm
4. Das Licht zum Narren halten führt uns auf die Sammellinse
(Feynman S. 70 ff. Abb.35, 36; Bader
Info: Lichtausbreitung im Vakuum mit l Vak; in der Materie (z.B. Glas) mit l Glas
Feynman Abb. 35, 36; Zeigeraddition für die Sammellinse: Wir können der Natur einen Streich spielen und das Licht auf dem kürzesten Weg (S-M-P) verlangsamen: Wir brauchen nur Glas von der jeweils richtigen Dicke einzuschieben, damit das Licht auf allen Wegen gleich lang braucht. Das hat zur Folge, dass alle Pfeile in die gleiche Richtung weisen und einen langen, resultierenden Pfeil ergeben – eine Menge Licht! Eine Sammellinse ist also ein Glas, das die Wahrscheinlichkeit erhöht, dass Licht von einem Punkt zu einem anderen gelangt.
Einen sehr geschickten Zugang zu den Inhalten "Sammellinse und Auflösungsvermögen" bieten die Programme Bader
An die Nichtlaien,
d.h. an jene Physiker/innen, die mit den Altlasten der Quantenelektrodynamik behaftet sind:
Steckenrad = rotierender Zeiger = lambda-Zähler = Phasenanzeiger = komplexe Wahrscheinlichkeitsamplitude = Übergangsamplitude = Ereignisvektor = Psi -Darsteller = fiktive Stoppuhr
Ist das hier präzisierte Konzept (Zeigerformalismus ) eingeübt, können Schülerinnen und Schüler sich mit dem von Bader zusammengestellten Programm in weite Bereiche der Quantenphysik selbständig einarbeiten. Auch Themen wie Holographie und Bragg-Reflexion sind fürs Selbststudium aufgearbeitet.
Nicht auch Lust zum Schmökern? Es soll allerdings nicht verschwiegen werden, dass die DOS-Oberfläche des Programms einem bisweilen Selbstdisziplin abverlangt.
In einem rotierenden Zeiger steckt die gleiche Information wie in einer "ganzen Welle". Die Überlagerung von Wellen wird durch die Zielpunktfestlegung und die dortige Zeigeraddition realisiert. Das huygensche Prinzip (Wellenfronten als Summe von Elementarwellen bzw. die Elementarwellen-Sichtweise überhaupt) findet Eingang über die Modellanweisung "Finde alle möglichen Zeigerlinien". Quantenobjekte werden über komplexe Wahrscheinlichkeitsamplituden Psi erfasst, denen keine anschauliche Bedeutung zukommt, die jedoch über die Schrödingergleichung streng determiniert sind. Die Stochastik tritt erst bei der Wahrscheinlichkeitsdeutung von |Psi |2 auf. Das Quadrat dieser Wahrscheinlichkeitsamplitude ist über das Quadrat des resultierenden Zeigers im Ziel zu finden.
Das Modell darf nicht mit der Realität des Naturvorgangs identifiziert werden. Sonst entsteht Erklärungsbedarf, wo nichts erklärt werden kann. Es fliegen keine rotierenden Pfeile zwischen Q und Z! Magnetische Feldlinien sind auch nur Denk- und Anschauungshilfen, denen keine Realität im engeren Sinne zukommt. Jedes Erklären in der Physik ist ein Modellieren der Wirklichkeit, dies geschieht auch hier.
Feynman: Das Warum versteht niemand. Ich kann nicht erklären, warum sich die Natur so und nicht anders verhält (Lit. 2 S. 20, 23, 143) Photonen sind keine Individuen, deren Lebensweg sich verfolgen lässt. Nur bei Geburt und Tod erscheinen sie dem Experimentator als lokalisierte Körperchen.
Newton über das Gesetz der Massenanziehung: Ich habe noch nicht dahin gelangen können, aus den Erscheinungen der Schwere den Grund dieser Erscheinungen abzuleiten, und Hypothesen erdenke ich nicht. In unserer heutigen Sprache: Warum Massen sich anziehen, wissen wir nicht!
Kübelbeck: Die Quantenphysik zeigt uns: es gibt keine Realität an sich, es gibt nur, was wir beobachten. Wir treten einer Sache immer als Subjekt gegenüber. Damit sind unsere Bilder von der Natur die einzige eigentliche Wirklichkeit ... – eine faszinierende und menschliche Wirklichkeit.
Literatur:
Bader, Franz: Eine Quantenwelt ohne Dualismus Schroedel Hannover (1996) DM 61,41 Buch und Programm; Unterrichtsgang mit (sich selbst erklärenden) DOS-Programmen und Arbeitsblättern.
Feynman, Richard P.: QED - Die seltsame Theorie des Lichts und der Materie; Piper München, Zürich (1992) DM 16.80 Inhalt: Photonen und Elektronen als Quantenobjekte; für interessierte Laien geschrieben.
Kübelbeck, Josef: Modellbildung in der Physik insbesondere in der Quantenphysik; LEU Heft Ph 22; Landesinstitut für Erziehung und Unterricht Stuttgart (September 1997) Moderner Unterrichtsgang zur Quantenphysik; hier wurden die meisten Graphiken entnommen.
Treitz, Norbert: Computerprogramme zur Physik, Deutsches Institut für Fernstudium (DIFF) Tübingen
Zur Einführung in den Zeigerformalismus geeignet.
Spektrum der Wissenschaft – Digest: Quantenphänomene 1/1999 Neue, interessante Artikel zum Titelthema, z.B.: wechselwirkungsfreie Messungen.